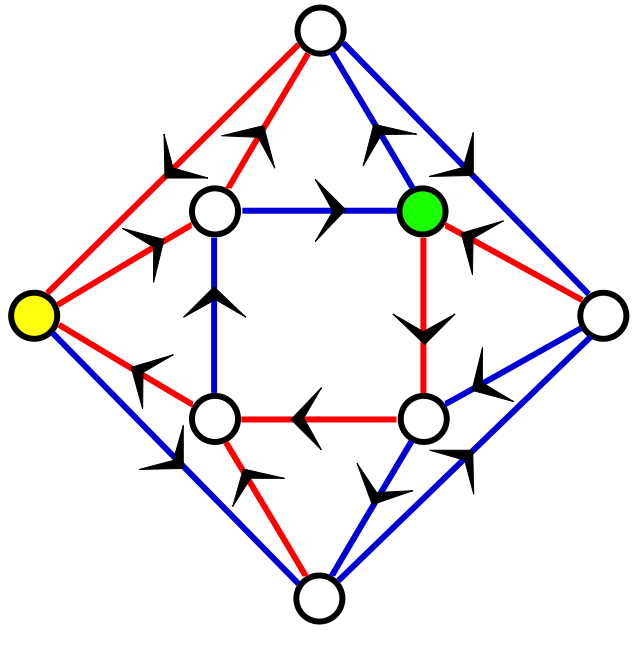Bất kể bạn bắt nguồn từ đâu, bằng việc đi theo chỉ dẫn Xanh-Đỏ-Đỏ--- Xanh-Đỏ -Đỏ --- Xanh-Đỏ-Đỏ, bạn sẽ đến được đỉnh màu Vàng. Bài toán ban đầu là một giả thuyết, cho rằng luôn có một chỉ dẫn tổng quát để đến một vị trí cần đến, trong một hệ đóng mà ở đó không có con đường nào rẽ ra ngoài.

Bài toán này có nhiều điểm giống với Định lý Bốn Màu (Four Colour Theorem) chưa được chứng minh, ở đó cho rằng bạn chỉ cần duy nhất 4 màu để có thể tô vào mỗi tỉnh thành một màu sao cho hai tỉnh kề nhau sẽ có hai màu khác nhau. Các bạn có thể tìm hiểu thêm về bài toán này qua bài viết bằng tiếng Anh The origins of proof IV: The philosophy of proof. Bài toán này lần đầu tiên được sự quan tâm rộng rãi là vào năm 1852; và năm 1879 Alfred Kempe đã công bố " chứng minh" của mình trên tạp chí Nature và cả tạp chí toán học Mỹ, American Journal of Mathematics. Đáng tiếc, năm 1890, Percy Heawood đã tìm ra một lỗi sai ở chứng minh trên, và phải đợi 86 năm sau, Kenneth Appel và Wolfgang Haken mới đưa ra được một chứng minh liên quan đến bài toán này bằng phép tương phản. Chứng minh bắt đầu bằng giả thuyết có nhiều bản đồ địa lý 5 màu, bạn luôn có thể chọn ra một bản đồ có số tỉnh thành là nhỏ nhất. Sau đó họ chỉ ra rằng tấm bản đồ đó phải chứa một trong số 1936 cấu hình khả năng, và họ chứng minh được rằng mỗi câu hình đó có thể rút gọn để tạo thành các mẫu nhỏ hơn, và có thể được tô bằng 5 nằm khác nhau. Điều này là mâu thuẫn bởi vì chúng ta đã đặt ra giả thuyết rằng tấm bản đồ năm màu ban đầu là nhỏ nhất.

Vấn đề với chứng minh của họ đó là sử dụng máy tính để phân tích 1936 cấu hình khả năng của bản đồ. Chứng minh đó nếu in ra sẽ rất dài và không nhà toán học nào có thời gian và khả năng để đọc hết được bản in này. Nếu một chứng minh mà không được kiếm chứng, thì đa số các nhà toán học cho rằng nó không phải là một lời giải tường minh.

Ngược lại với chứng minh của Định lý 4 màu, lời giải bài toán Con đường màu của Trakhtman được xem là đơn giản, tao nhã và tinh tế. Trakhtman đã giải bài toán bằng phương pháp truyền thống - không sử dụng đến máy tính - mà bằng bút chi và giấy trắng. Công trình của Trakhtman còn có ý nghĩa hơn vì nhờ nó mà ông được công nhận là giáo sư toán học tại trường đại học Bar-Ilan. Là một nhà khoa học Nga, nhập cư vào Israel năm 1990, Trakhtman đã phải làm việc không mệt mỏi để duy trì vị trí của ông, nhằm nhận được biên chế chính thức của trường đại học. Lời giải của bài toán này còn có nhiều ứng dụng cho lĩnh vực bản đồ cũng như khoa học máy tính. Bạn có thể xem trước lời giải của Trakhtman trên trang dự bị arXiv.

Nguồn : plus.maths.org